La entropia como creadora de orden

Arturo Sirvent Fresneda

25/05/2020

La entropia como creadora de orden
Seminario optativo física estadística
Universidad de Granada

---

Abstract: Vamos a profundizar no en el tema de entropía como cantidad de macroestados mas que como desorden del sistema. Luego hablaremos sobre la energía libre de Helmholtz y como puede el principio de mínima energía ayudarnos a enterner las transiciones de fase desde un punto de vista termodinámico. Por último trataremos el tema de las interacciones entrópicas y como es posible que elementos de un sistema sin interacción directa entre ellos, muestren un comportamiento conjunto.

Referencias:

En la teoría me he basado mayormente en el artículo de José A. Cuesta (La entropía como creadora de orden), la mayoría de lo que diremos aquí está en ese artículo, pero he intentado desarrollar un poco más conceptualmente la idea, para que sea más presentable. Los desarrollos matemáticos se llevan a cabo en dicho artículo.

También teneis en youtube un video de QuantumFracture que habla sobre este tema y está muy bien.

Introducción:

Vamos a revisar un tema bastante delicado, en el sentido de que si te lo preguntaran sería dificil exponer diferencias concretas, es el tema de caos y desorden. Sabemos que no es lo mismo y que hay sutilezas, pero tendemos a asociarlos, Las sutilezas las encontramos en la ecuación que vemos aquí abajo, la ecuacion de Boltzmann. Hacemos esta asociación pues a mayor desorden mayor numero de microestados pero veremos como es posible que un sistema aumente el número de microestados mediante una estructura ordenada.

Concepto de entropía:

Imaginemos que tenemos un sistema tal que nuestros microestados se caracterizan por la orientación de unas flechas. Esto no tienen porque ser espines (que podrían), alomejor son dos estados energeticos de un atomo, o dos formas de ocupar niveles energeticos etc. Pero para simplificar, vamos a tomar el ejemplo de los espines. Estos, bajo unas condiciones externas reaccionan y toman una configuración. Se ven claramente influenciados por sus condiciones, que podríamos decir que ahora es un campo magnetico muy fuerte.

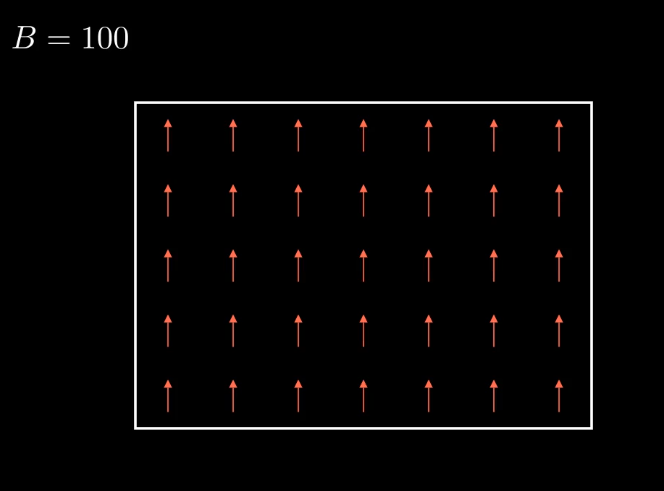
Sin embargo si relajamos las ligaduras del sistema y le dejamos que evolucione libre, vemos que adopta nuevas configuraciones(por ejemplo aquí cambian mas o menos la mitad de ellos) , que antes no veíamos o veíamos muy raramente.

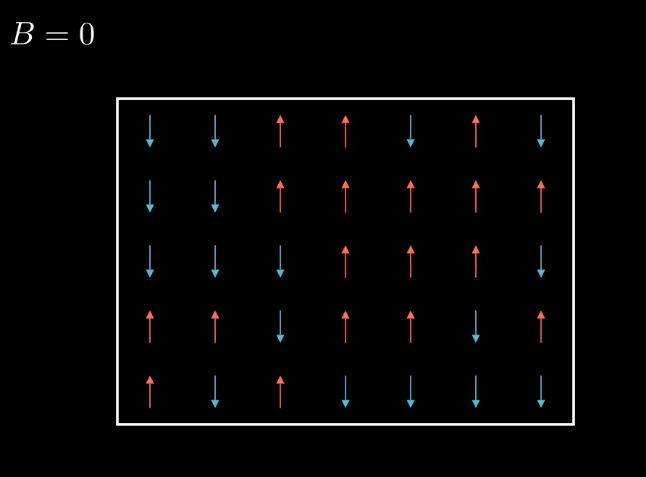
Ahora tenemos muchas configuraciones posibles compatibles con nuestro macroestado.
Esta es nuestra colectividad, el conjunto de todas ellas, siendo además todas equiprovables por el principio de igual probabilidad a priori.

Tenemos muchas muchas más de las que aparecen aquí. Entre ellas estan tanto la que esta completamente alineada (todas las flechas UP), como la que solo tiene la mitad (mitad UP, mitad DOWN) y tiene un promedio nulo de flechas arriba.
Repito, todas las configuraciones ahora son equiprobables, hemos relajado el sistema y no hay razon para pensar que la configuraciones que teniamos en B=100 es mas probable que cualquier otra. (Con el campo activo, sí teníamos razón para pensarlo).
A continuación vemos un frame del video de QuantumFracture, que nos muestra porqué es más probable observar el estado en unos macroestados que en otros, es basicamente por la gran cantidad de microestados compatibles.

Hace también una apreciación muy interesante, dado un microestado, con una configuración muy peculiar como podría ser la forma de un cocodrilo o un dragón.

Esta configuración no nos parece desordenada, pero sin embargo tiene una alta entropía, esto es debido a la que esta configuración es una de las miles que pueden formar al macroestado mas probable, el de 0 flechas promedio.no podemos guiarnos por un concepto intuitivo de entropía. (Más adelante definiremos que es orden en nuestro caso.)

Entropía máxima:

Si nuestro sistema se encuentra en un baño térmico, entonces la temperatura es una constante del sistema, pero la energía de nuestro sistema ya no es constante, lo que si es constante es la energía media, (la energía interna) \(<E>\) .

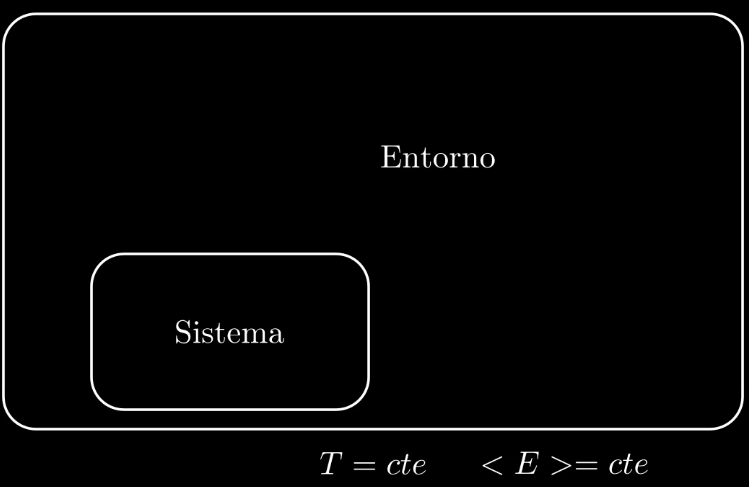
Esto último supone una restricción sobre nuestro sistema, de la misma forma que lo suponía el campo magnético en el ejemplo de los spines, no siempre será posible alcanzar la entropía máxima la cual se alcanza en ausencia de restricciones.
El nuevo valor que obtiene un máximo es la entropía menos \(<E>/T\), esto lo deducimos de la termodinámica. \(S-\frac{<E>}{T}\)

Energía libre en un sistema isotermo:

Recordemos que nuestro sistema es isotermo y tenemos dos constantes limitándonos los estados accesibles. \(T=cte\) \(<E>=cte\) De la termodinámica también sabíamos que el calor tenía esta expresión: \(Q=TS\) Si sustituimos en la expresion queda: \(\frac{Q-<E>}{T}\)

En el artículo de Jose A. Cuesta se indica muy acertadamente que *“si no hay restricciones se maximiza \(Q\), si hay restricciones lo que se maximiza es \(Q- <E>\). El término del numerador (\(\frac{Q-<E>}{T}\)) es justamente (menos) la energía libre de Helmholtz $(F)$. \(Q-<E>=-F\) Básicamente se interpreta como la parte de energía del sistema que puede convertirse en trabajo.

De esta expresión podemos hacer la siguiente apreciación para un sistema isotermo:

Esto supone que un aumento de la entropía implica (recordemos que T es constante) un aumento del calor y una disminución de la energía libre del sistema.
De esta manera, hemos demostrado que para un sistema isotermo el principio de máxima entropía es equivalente al principio de mínima energía libre.

Es claramente consecuencia de la maximización de la entropía (segundo principio de la termodinámica), pero es más característico e intuitivo ver que debido a este principio obtenemos:

• Estado muy homogeneo energeticamente hablando.

• Pocas diferencias de temperatura (sin flujo de calor no se puede obtener trabajo).

• Muerte térmica del Universo

Mecanismo general de las transiciones de fase:

Ahora vamos a hablar de la una transición de fase general, vamos a ver bajo que condiciones el paso a una fase ordenada son favorables, esto sucede en la naturaleza, por ejemplo la cristalización del agua, bajo condiciones de temperatura baja.

Vamos a definir que tenemos dos estados, uno ordenado y uno desordenado, como ya hemos indicado ¿que es ordenado?, bueno por ahora vamos a suponer una configuración intuitiva en la que hay equidistanciamiento o una disposición geométrica que minimiza fuerzas de interacción etc… (Además recordeos que cada fase del sistema tiene sus variables. \(S\), \(F\), \(<E>\equiv E\)).

Aqui vemos unos ejemplos de lo que podría clasificarse como desordenado (izquierda) y lo que podría entenderse por ordenado (centro y derecha). Repetimos, es un poco arbitrario este concepto de orden por ahora.

Ahora definidmos las diferencias de las contidades \(S\), \(F\), \(<E>\equiv E\) entre la fase inicial (desordenada) y la fase final (ordenada) (esta electrión ha sido arbitraria, pero ahora tenemos que ser consecuentes). \(\Delta E = E_{O}-E_{d}\) \(\Delta F = F_{O}-F_{d}\) \(\Delta S = S_{O}-S_{d}\) Usando la ecuación conocida de la energía libre $F=E-TS$, podemos expresar una relación sencilla entre las diferencias. \(\Delta F=\Delta E-T\Delta S\)

Ahora nuestro objetivo es revisar las posibles combinaciones.(Recordemos que el estado final es el ordenado.)

Si la fase ordenada (final) tiene menor energía libre entonces es más favorable/propicia el estar en la fase ordenada. \(\Delta F <0\)

Si es positiva la difetencía es positiva: \(\Delta F>0\) es debido a que F a aumentado y eso lo hace menos favorable el cambiar de fase a la fase ordenada.

Aclaración:Tenemos que entender que ahora estamos tratando con las diferencias de dos fases de un sistema, pero no estamos considerando la transición ni nada, lo estamos estudiando como un sistema en el equilibrio, luego el hecho de que la entropía se reduzca y F también no está violando la segunda ley de la termodinámica, pues habría que estudiar el caso mediante termodinámica del no equilibrio, estamos realizando una aproximación aproximada, no siempre se cumple.

Es lógico pensar que en un caso típico y siguiendo la intuición, que la energía interna del sistema se minimiza en un estado ordenado debido a que los componentes se posicionan de una forma más óptima. También podemos suponer que en el caso típico, esto supone una reducción de los microestados posibles, y se reduce la entropía.
Tenemos por un lado a la energía contribuyendo a que \(\Delta F\) sea negativo a la entropía contribuyendo a que sea positivo.
Hay muchas comportamientos posibles, pero aquí viene lo interesante, si reducimos la temperatura, el segundo miembro se hace muy pequeño \((T \Delta S)\) y \(\Delta E\) logra que \(\Delta F\) sea negativo (esto no es valido siempre pues puede que Delta E tambien dependa de la temperatura y se contrarresten excepto para $T=0$, pero puede no suceder), en términos generales este es el origen termodinamico de las transiciones de fase.

Pero que pasa en el caso que no haya interacción entre los componentes: \(\Delta E=0\) Ahora tenemos: \(\Delta F = -T \Delta S\) Pues la única alternativa para la cristalización $(\Delta F<0)$ es : \(\Delta S>0\) \(S_O>S_d\) Que la entropía en la fase ordenada sea mayor que la de la fase desordenada. Esto es lo que hemos estado buscando desde el principio, vamos a ver como puede lograrse esto mediante un ejemplo concreto.

Esferas duras:

Se trata de un gas de esferas duras neutras que no muestran ninguna interacción entre ellas. La propia característica de no poder solaparse y ser objetos extensos va a provocar que bajo ciertas condiciones se ordenen y esto aumente la entropía.

Si las tenemos en un volumen, el espacio libre para colocar otra esfera no es el volumen total menos el volumen que ocupa cada esfera: \(V-N*\nu_{esfera}\)

Pues las esferas son objetos rígidos y no podríamos moldearlo para que cupiera en dicho espacio. debe haber una region de espacio para que la esfera se coloque propiamente.

Por ejemplo en esta imagen, no cabría otra esfera.

Tenemos una zona entorno a cada esfera, donde no cabe otra (otro centro de esfera), pues solaparían:

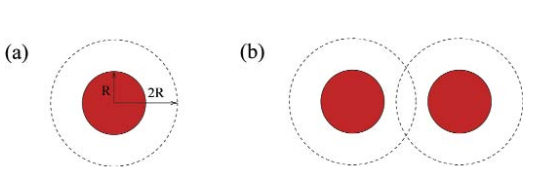
De forma que el espacio realmente accesible es:

\[V-N*\nu_{esfera}^*\]

con esa \(\nu_{esfera ^*}\) el volumen de la esfera de radio doble.

Fuera de los radios de exclusión sí podemos añadir otra esfera. (Estamos ignorando los efectos de estar en un contenedor finito, pero no pasa nada pues en la práctiva es como si fuera “infinito” en comparación con el tamaño de las esferas (coloides)).

Pero, ¿y si están cerca??
Pues cuando se acercan, el área prohibida se solapa.

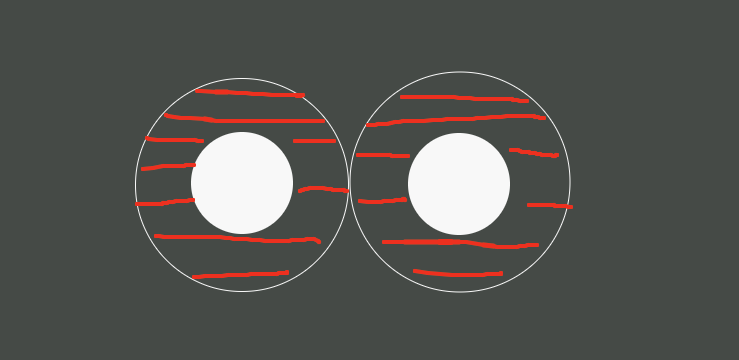
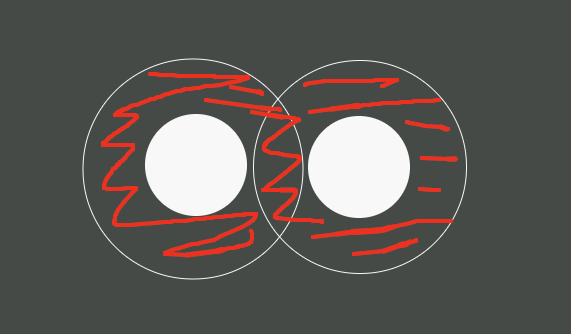
De modo que si la densidad de esferas es alta y empiezan a juntarse de la manera correcta (de aquí viene nuestra defición concreta de orden), esto resulta en una reducción del área prohibida, pues entre ellas comparten área restringida para que haya otra. Esto aumenta el area accesible para otras esferas, esto aumenta el número de configuraciones y esto aumenta la entropía. La ordenación que aquí experimente será aquella que maximice el área accesible, esto es nuestra definición de orden (pues dijimos al principio que el orden es un poco relativo, en este caso es eso). Es la entropía la que posiciona a las esferas.

Ya hemos demostrado que la unión de las esferas en patrones geométricos que minimicen adecuadamente logra aumentar las configuraciones y consecuentemente la entropía.

Apunte:Esto puede parecer ser cierto solo coloides etc… Sin embargo si vemos a las moléculas o átomos como esferas con un radio de exclusión efectivo, es decir: Su repulsión les proporciona algo semejante a un volumen de exclusión extenso, como podría ser una pelota. Pues conforme la temperatura baja, las energías cinéticas bajan y se puede penetrar menos en esa area de exclusión. Esto es equivalente a que el radio de la pelota aumente. Es por esto que no hace falta precisamente coloides duros para ver esta ordenación, conforme las esferas se hagan mas grande porque bajamos la temperatura, los radios aumentaran y las esferas / partículas / moléculas se reordenarán de una manera geométrica que minimize sus interacciones.

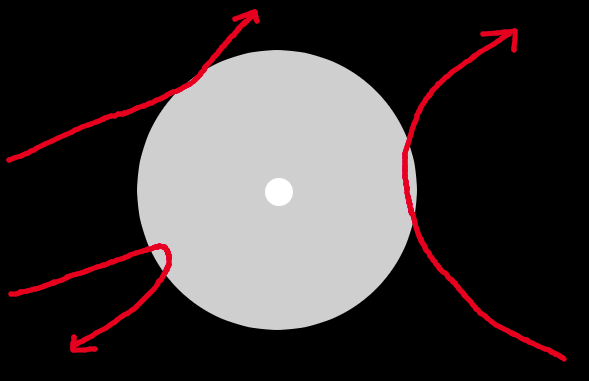
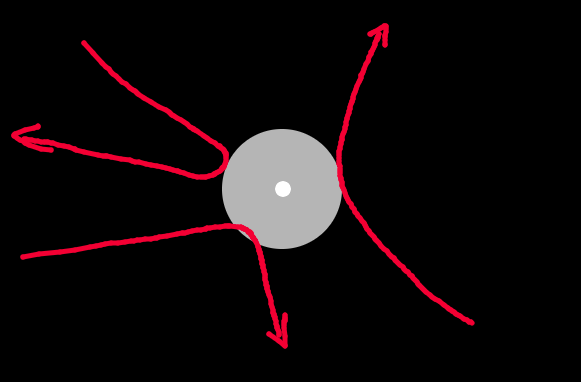
En esta imagen vemos como el radio efectivo de exclusión es mayor conforme baja la temperatura pues la energía cinética de las partículas no les permite penetrar más, al aumentar sus radios debido a la reducción de la temperatura, la densidad aumentará y responderán al mismo principio que hemos descrito de maximizar área accesible y cristalizar.

Interacción entrópica:

Por último vamos a hablar de la interacción entrópica, vamos a ver como parece haber un potencial atractivo, que es creado unicamente por el principio de maximizar la entropía.

Imaginemos que tenemos dos componentes posibles, esferas grandes y esferas pequeñas.

La mezcla de ambas tiene mayor entropía que ambas separadas (fenómeno estudiado por Gibbs), pues supone mas microestados. Pero por otro lado, si las partículas grandes se agrupan todas juntas, sus regiones de exclusión se solaparán, con la consiguiente ganancia en volumen accesible a las pequeñas, y a mayor volumen accesible, mayor entropía. Así que la primera contribución tiende a mezclar los dos componentes, mientras que la segunda tiende a segregarlos.
Tenemos un contribución a la entropía debido a la mezcla y otra debido a la separación de ambos componentes.
La solución es que el balance final dependerá de las densidades de ambos componentes.

Podemos observar dos casos concretos, el primero (izquierda), tenemos densidad de esferas pequeñas baja luego el sistema se mezcla. En la segunda (derecha) tenemos una alta densidad de esferas pequeñas, eso hace segregar las esferas grandes, induce una separación de estados.

Como curiosidad mencionar el efecto de la convección granular o más técnico segregación por tamaño en un medio granular vibrante:

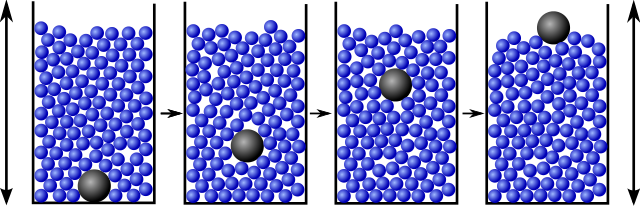
Bueno basicamente es esto que se ve en la imagen, al agitar el medio, este se reordena. Esto no es exactamente lo que estamos tratando en este artículo pues aquí tambien hay que tener en cuenta minimización de la energía potencial gravitatoria, efectos de conveccion etc… Sin embargo tienen también un efecto de segregación según componentes y me parecía curioso, lo podeis probar con arroz y garbanzos.

Ejemplo de sistema en red:

Esto que vamos a ver a continuación es un ejemplo concreto como el de las bolas de diferente radio. Vamos a estudiar en este caso discreto como son las intereacciones entrópicas entre los componentes.

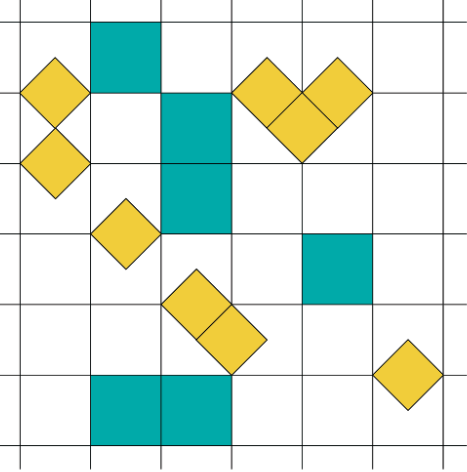
Se trata de modelar un sistema como el que hemos comentado con dos tipos de partículas. Tenemos los cuadrados y los rombos.

Queremos describir el sistema mediante la colectividad macrocanónica pues el número de cuadrados y rombos no es fijo, va variando.
En nuestro caso no tiene sentido perder tiempo en analizar el desarrollo matemático llevado a cabo, pero dicho desarrollo completo está en el artículo de José A. Cuesta. Vamos a indicar nada mas que las expresiones clave.
Usamos el formalimos macrocanónico como hemos indicado:

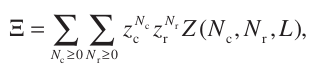
Tras hacer unas manipulaciones obtenemos esta nueva forma para la funcion de partición macrocanónica (los terminos iniciales son las fugacidades):

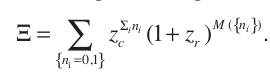
Despejando \(M({n_i})\) y haciendo unos cuantos cambios de variable para que se nos haga mas facil la comparacion con el gas de red de Ising:

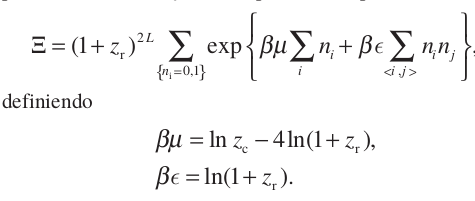
Podemos estudiar la fenomenología de este caso a partir del modelo ferromagnetico de Ising cuya funcion de partición es:

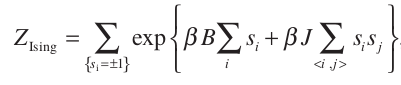
Tras hacer la comparación con dicho modelo ferromagnético obtenemos las siguientes conclusiones:

• Tenemos un sistema con interacción dura que se ordena conforme aumenta la entropía.

• La diferente forma que tienen de ocupar el espacio los componentes hace que se optimice / se ordenen para lograr mas espacio ocupable.

• Se crean agrupaciones o clusters por mera interacción entrópica. Es decir, el efecto resultante es una transición conocida como segregación o separación de fases.

Gracias a que hemos obtenido una comparativa entre nuestro sistema y el gas de red de Ising, podemos estudiar comportamientos que a priori no esperaríamos que tuviera por no haber potencial de interacción:

• La equivalencia nos dice que el sistema inicial se comporta como si los cuadrados experimentaran una interacción atractiva efectiva, cuya intensidad está directamente relacionada con la densidad de rombos (a más densidad de rombos mayor atracción).
  La entropía induce interacciones efectivas entre las partículas.

• Concretamente, la interacción atractiva que experimentan las partículas coloidales como consecuencia de aditivos añadidos al coloide (típicamente polímeros), recibe el nombre de depleción.

• La depleción tiene muchas aplicaciones industriales por ejemplo, se puede limpiar el agua de restos de pintura mediante la adición de polímeros (las partículas de pintura se agregan y precipitan al fondo).

Se ha llevado a cabo una simulación del fenómeno. Esta simulación se ajusta mediante unas probabilidades de “nacer” o “morir” para cada uno de los componentes del sistema. Mediante este método podemos dar libertad de movimiento a los componentes del sistema, así dejar que “intereactuen” y se ordenen.
Tras ajustar los parámetros para un punto crítico en que se produzca una coexistencia de fases rombo / cuadrado, dejamos al sistema evolucionar desde un estado en que los cuadrados se encuentran solitarios y muy repartidos:

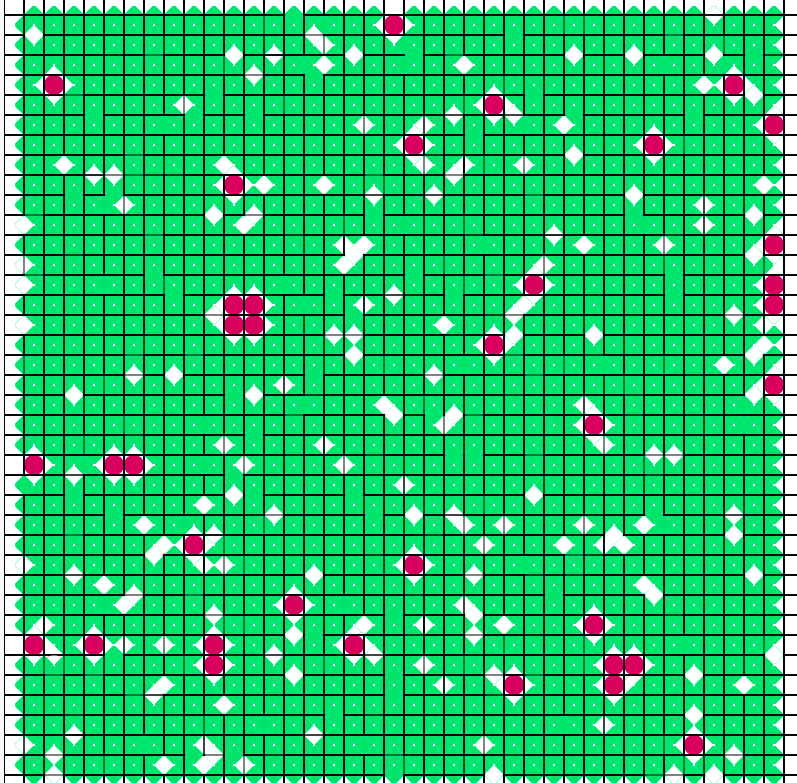
Tras dejar que evolucione un tiempo, vemos como se forman cúmulos de cuadrádos como si se atrajeran (derecha).

Aquí vemos otra simulación:

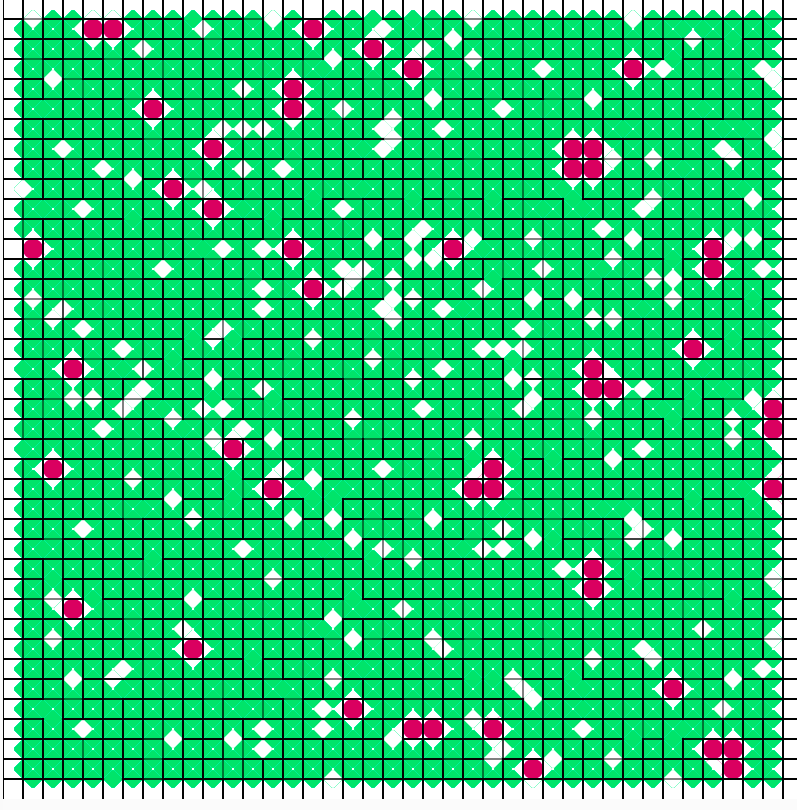
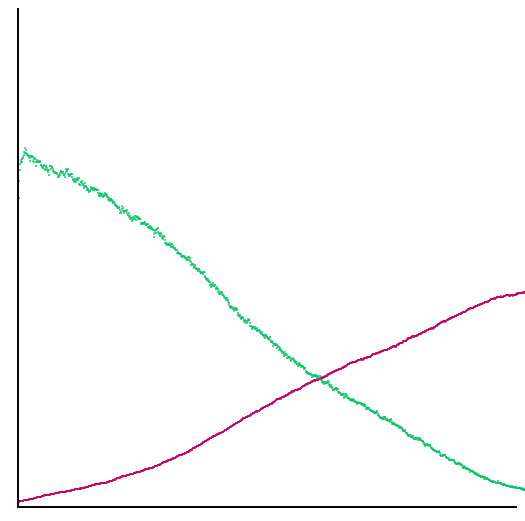
De nuevo podemos ver como se produce este efecto de acumulación en grupos. Si representamos la cantidad de cada uno de los colores según el
tiempo de evolución del sistema, vemos lo siguiente.

Y la evolución del sistema se puede observar en el siguiente link.

Recursos:

A continuación indico los recursos usados en este artículo:

• Artículo de Jose A. Cuesta (La entropía como creadora de orden)

• Video de Quantum Fracture (El cristal que se ordena solo.)
  $https://www.youtube.com/watch?v=FpA_FhJQXzI$

• Simulaciones realizadas:
  $https://editor.p5js.org/ArturoSirvent/sketches$

• Repositorio en GitHub con todo el código relativo a la presentación (realizado con Manim):
  $https://github.com/ArturoSirvent/presentacion_entropia$